Windows10系统自带照片应用显存泄露BUG
系统一直是保持更新最新版本的,出现问题的版本:
- Windows 10 18362.239
- Microsoft 照片 2019.19051.16210.0
出现场景:
打开了一个png图片后最小化至后台,过了大约一两个小时后显卡显存占满,系统严重卡顿
检查发现照片应用占用了7G的显存:
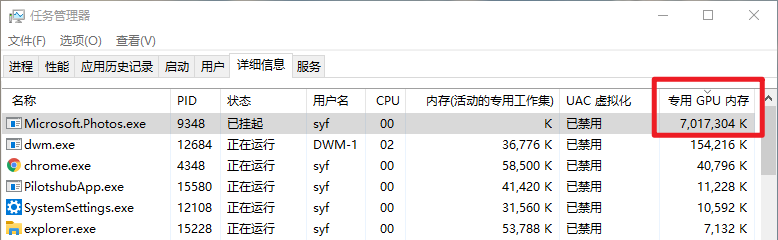
已经第二次出现了,应该算比较严重的BUG了
系统一直是保持更新最新版本的,出现问题的版本:
出现场景:
打开了一个png图片后最小化至后台,过了大约一两个小时后显卡显存占满,系统严重卡顿
检查发现照片应用占用了7G的显存:

已经第二次出现了,应该算比较严重的BUG了
上周发了个博客说多分类应该用一个像素代表不同值的方式来实现,今天又仔细研习了一下 github 上这个 issue,看了作者的回复,感觉还是应该用多通道作为输入。
于是我把unet传入的n_classes参数改成了2,然后让传入的数据形状和unet输出预测的形状一致,把嗅球和白色区域数据用torch.cat叠起来,最后两个通道输出扩充一个通道保存成3通道RGB的形式

经过上周的努力,嗅球识别模型的命中率已经比较可观了,但是误判率还是比较高。上周五老师给了我一份新数据,标注的是包括嗅球的周围白色区域的标签,类似下图蓝色部分:
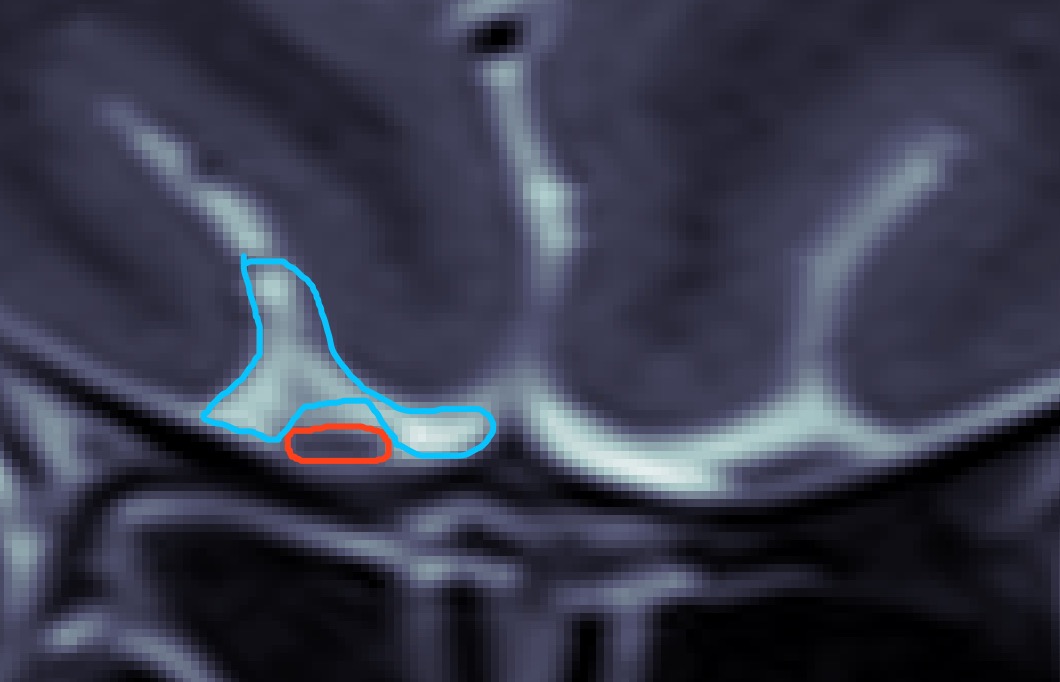
然后我产生了初步的利用白色区域标签的想法,即像训练嗅球那样训练出分割白色区域的模型,然后对于一张验证图片,分割出如上图所示的蓝色标签(白色区域)和红色标签(目标嗅球区域)。先前的嗅球区域会有一些错误并且偏离较大的预测,暂时简单的想法在识别出的白色区域下方设置一个阈值,超过这个阈值的预测认为是无效预测
接下来的问题就是像训练嗅球数据集一样训练白色区域的数据集了。我一开始的想法就是像训练嗅球一样,把nii数据转化成png之后一样的代码再训练一遍就是,但是仔细想想,既要训练嗅球,又要训练白色区域,这很明显是一个多分类问题,U-Net网络本来就支持多分类识别,那我是否可以在原来的代码基础上改动下输入的channel和class数呢?
这周主要尝试的是裁剪中间320x320区域,输入网络后使用focal loss作为loss function进行训练。一开始也尝试了BCE loss,因为**兄发的focal loss有一些小小的python版本兼容问题,而我之前在GitHub上看的一个UNet是用BCE loss,然后就一边弄focal loss的代码一边服务器上先跑着torch自带的BCE loss看看效果。但是BCE loss的结果出来并不是很好,后面就都用focal loss跑了
尝试了学习率lr=0.0001和lr=0.00001,因为图片被裁剪的相对原图比较小,所以也尝试了batch size=8的训练。在此之前我只知道这个超参数是指每次喂入网络的样本数,并不知道其对训练轮数有什么样的影响,查了相关资料后知道了epoch、 iteration和batch size这三者的关系:
以及一篇比较好的讲解:
深度学习中的batch的大小对学习效果有何影响? - 程引的回答 - 知乎
https://www.zhihu.com/question/32673260/answer/71137399
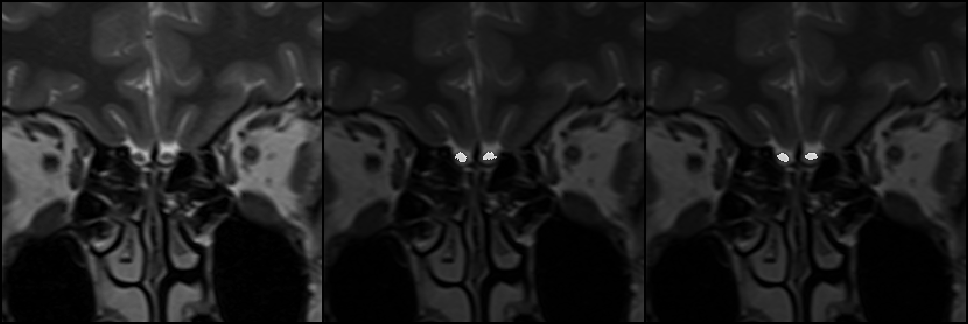
最后训练出来lr=0.00001时后面迭代次数比较高的checkpoint比较好,下面是batch size=4时迭代第30000次的结果中的一张图,大部分分割结果都和下图类似:
朋友,想必你最近登录微软、谷歌的时候已经注意到,输入用户名和密码的逻辑似乎和先前不大一样了。当你熟练地敲下你那文艺的用户名,左手小拇指轻轻按下 tab 键,诶???说好的密码框呢?最近看到一篇文章 Why are the username and password on two different pages? 比较好的阐述了这个转变的缘由。
