分布式定时任务 xxl-job 优雅关闭问题
执行器下线时的destroy逻辑
step 1. onDestroy
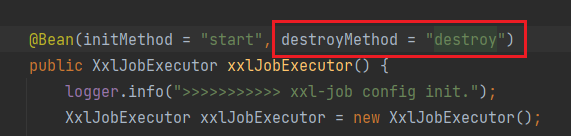
step 2. stopExecutorServer
先销毁了web容器,销毁后无法接受调度,然后再从注册表中下线,没有主动先下线

先销毁了web容器,销毁后无法接受调度,然后再从注册表中下线,没有主动先下线
生产环境前段时间neo4j图数据库总是在凌晨定时任务删除过期节点时报内存占用过高的告警,研究下怎么配置参数:
neo4j内存结构:
OS保留:OS内存、Lucene索引缓存
页面缓存:图数据缓存、索引缓存
jvm堆:图查询、图管理、事务状态(可选)
事务状态
neo4j memory management
推荐的内存参数:
分配了3.6G jvm堆内存,2G 页面缓存,剩余2.6G空闲内存和 native memory 给 Lucene 和 Netty
一个收获:很多中间件jvm内存并不是一定需要占大头,例如某些MQ和缓存会使用 native memory 来避免jvm频繁垃圾回收带来的性能问题;以及像neo4j的Lucene引擎使用系统分页缓存
三个建议:
索引文件太大时,多剩点内存给OS
并发事务和update语句越多,分配的jvm堆内存也要越大(别超过31G)
jvm堆内存设置初始值和最大值一致,因为jvm更改堆大小时会触发full GC影响性能
syf@syf-ubuntu ~/o/neo4j-community-3.5.8 [1]> bin/neo4j-admin memrec --memory=8g
WARNING: Max 1024 open files allowed, minimum of 40000 recommended. See the Neo4j manual.
# Memory settings recommendation from neo4j-admin memrec:
#
# Assuming the system is dedicated to running Neo4j and has 8g of memory,
# we recommend a heap size of around 3600m, and a page cache of around 2g,
# and that about 2600m is left for the operating system, and the native memory
# needed by Lucene and Netty.
#
# Tip: If the indexing storage use is high, e.g. there are many indexes or most
# data indexed, then it might advantageous to leave more memory for the
# operating system.
#
# Tip: The more concurrent transactions your workload has and the more updates
# they do, the more heap memory you will need. However, don't allocate more
# than 31g of heap, since this will disable pointer compression, also known as
# "compressed oops", in the JVM and make less effective use of the heap.
#
# Tip: Setting the initial and the max heap size to the same value means the
# JVM will never need to change the heap size. Changing the heap size otherwise
# involves a full GC, which is desirable to avoid.
#
# Based on the above, the following memory settings are recommended:
dbms.memory.heap.initial_size=3600m
dbms.memory.heap.max_size=3600m
dbms.memory.pagecache.size=2g参考:
https://neo4j.com/docs/operations-manual/3.5/performance/memory-configuration/
https://neo4j.com/docs/operations-manual/3.5/tools/neo4j-admin-memrec/
kubectl有些操作比较冗长,又经常需要使用,所以写了几个别名,进测试环境pod终端方便些,鉴权自行解决
使用例:
# 进入终端
podl qa sox
# 展示pod列表
pods qa sox
# 进入pod的某个container,如istio
podn qa istio sox-58654c84d-lnk4f
# 查看stdout,这个基本没啥用,除非有的异步线程抛出异常没打到logback指定的文件里
podlog qa sox# >>> conda initialize >>>
# !! Contents within this block are managed by 'conda init' !!
eval /c/Users/enmonster/miniconda3/Scripts/conda.exe "shell.fish" "hook" $argv | source
# <<< conda initialize <<<
function podl --argument-names nmsp app
kubectl -n $nmsp exec -it (kubectl -n $nmsp get pod -l app=$app -o name) -c $app -- bash
end
function pods --argument-names nmsp app
kubectl -n $nmsp get pods | grep $app
end
function podn --argument-names nmsp container pod
kubectl -n $nmsp exec -it $pod -c $container -- bash
end
function podlog --argument-names nmsp app
kubectl -n $nmsp logs -c $app (kubectl -n $nmsp get pod -l app=$app -o name)
endJava 工程中注解配合切面往往能带来事半功倍的效果,但是注解有的时候并不是太灵活,例如方法注解无法指定一些自定义的参数,很多时候还是需要到方法里面去做一些侵入性的逻辑来完成想要的操作;为了解决这个痛点,我写了个 demo 通过反射+递归的方式来给方法注解提供解析动态参数的能力,例如对于 void doSomething(Entity entity) 这个方法,可以通过 @RecordEvent(code = "TEST", keyWord = "{entity.id}", content = "content is {entity.nested.foo}") 注解中的花括号来取到入参中 entity 参数的某些值,且支持无限递归获取子属性的值,demo 代码如下:
有这么两个参数类型,其中Entity类中包含类型为Nested的属性
@Getter
@Setter
@NoArgsConstructor
@AllArgsConstructor
public class Entity {
private int id;
private String name;
private String otherField;
private Nested nested;
}@Getter
@Setter
@NoArgsConstructor
@AllArgsConstructor
public class Nested {
private String foo;
private int bar;
}有一个方法,其第一个入参名为entity,可以使用“{entity.nested.foo}”这样的模板字符串,切面处理时会把模板字符串自动替换为对应入参属性的getter值,支持无限级往下查属性,查到最后的属性(本例中为foo)将其toString替换到模板。
@Override
@RecordEvent(code = "TEST", keyWord = "{entity.id}", content = "content is {entity.nested.foo}")
public void doSomething(Entity entity) {
int a = 2*2;
// some other logic
log.info("done");
}
public static void main() {
Entity entity = new Entity(1, "hello", "world", new Nested("bar", 111));
xxxService.doSomething(entity);
}调用时生成事件:EventPublishRequestDto(source=OPS, code=TEST, keyWord=1, content=content is bar, dateTime=2021-07-27T17:06:19.593)
具体方法是将模板参数用分隔符分割成队列,队列的第一个值是入参名,第二个值往后依次出队递归拿到文本对应的属性,以此类推直到队列为空,递归结束返回最深层的值
demo 源码如下:
本系列博客将介绍如何在家里搭建一个高可用的私有云。
现在家庭带宽运营商基本上都是不会给公网IP,都是在一个大局域网里通过类NAT协议映射出去,已节约运营商的IPV4资源。但是我们至少需要一个公网IP,你可以通过打运营商电话索要公网IP或买一台有公网IP的低配服务器(买IP送机器),两者优劣如下:
| - | 家宽申请 | 购买云服务 |
|---|---|---|
| 静态 | 否 | 是 |
| 带宽 | 高 | 低 |
| 时间成本 | 高 | 低 |
| 金钱成本 | 低 | 高 |
我已经有了一个腾讯云服务器的公网IP,但迫于服务器性能过低,带宽太小,还是和电信申请了个公网IP。上海电信打电话人工客服说明家里需要安装摄像头监控设施后第二天比较痛快地通知我已经帮忙开通了。
如果你的运营商不幸难以沟通,那只能考虑使用frp等穿透方案,走小水管公有云了。
拿到公网IP后,需要设置电信网关DMZ到内网路由器:
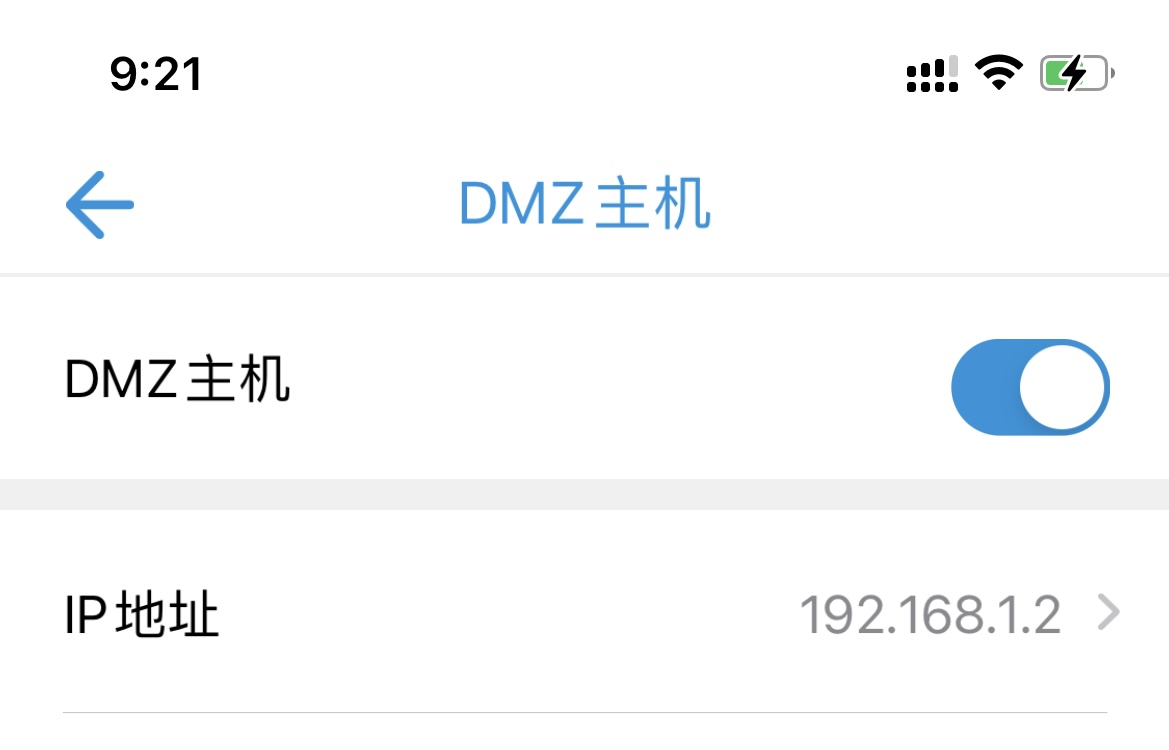
上海电信现在都是SDN网关了,封装了一些DMZ、UPNP、端口映射等功能到手机APP中;如果你的网关没有限制那么死,可以谷歌搜一下网关的型号,通过超管密码进到网关里面自己进行对应的设置,或干脆设置为桥接模式,桥接到二级路由上去,让路由器拨号。
我的路由器是192.168.1.2,直接把流量完整地DMZ到路由器上。至此,你的路由器已经能handle所有外部流量了(注意,因为不是桥接,现在路由器还是二级路由,没办法直接拿到公网IP)。